인공지능 기법을 이용한 고전수업의 학습효과에 대한 연구
Artificial Intelligence and Learning Effects of Reading Classics
Article information
Abstract
본 연구는 우리나라 대학의 고전수업에 대한 만족도에 대한 추정을 하기 위해서 인공지능을 기반으로 하는 머신러닝과 딥러닝 분석기법을 도입하여 학습변인에 따른 고전수업에 대한 만족도에 대한 분석을 하였다. 먼저 전통적 선형모형에 의한 회귀분석 결과, 가치관 형성, 영화감상의 고전읽기 도움, 토론의 유익성 등의 학습변인들은 모두 고전수업의 만족도에 긍정적인 영향을 미치는 것으로 나타났지만, 인공지능을 기반으로 하는 머신러닝인 의사결정나무에 의한 분석 결과, 삶의 가치관 형성, 영화감상의 도움, 대학생들의 국적, 고전읽기의 중요성과 고전의 필요성 등이 크다고 인식할수록 고전수업의 만족도가 크게 나타났다. 서포트 벡터 머신모형에 의한 분석결과, 결정계수가 조금 더 높게 나왔고, RMSE 도 낮아 모형이 좀 더 우수하게 나타났다. 딥러닝 모형의 심층 신경망 모형에 의해서 고전수업의 만족도에 대한 회귀예측을 하였을 때는 서포트 벡터 머신 모형보다 더 좋은 것으로 나타났다.
Trans Abstract
This study analyzes the machine learning and deep learning models that were used to forecast the satisfaction effect of classics reading classes. The following were the main findings of the comparison of their predictive abilities. First, the traditional regression model is somewhat low in coefficient of determinant. Second, the decision tree models predicts the satisfaction effect of classics reading classes better than the traditional regression model. Third, when we predict the learning effects of classics reading lessons, the support vector machine models show the high predictive power with the high coefficients of determination and low RMSE. Fourth, when we predict the learning effects of classics reading lessons, the deep neural network models also show the higher predictive power with appropriate epochs and batch sizes. Thus, since the machine learning and deep learning models can predict the satisfaction of classics reading classes more accurately, we need to adopt the machine learning and deep learning models to predict the satisfaction of classics reading classes using the learning variables.
1. 서언
현재 우리는 제 4차 산업시대를 맞이하여 살고 있다. 4차 산업혁명의 핵심은 데이터 기반혁신 기술인 빅데이터(Big data)와 인공지능(Artificial Intelligence; AI)이며, 여러 학문에서도 AI시대에 걸맞는 인공지능에 기반한 머신러닝(Machine Learning)과 딥러닝(Deep Learning) 기법을 도입하여 분석을 시도하고 있다. 그리하여 많은 학문분야에서 이러한 인공지능과 머신러닝 기법을 도입하여 분석하기 시작하고 있지만, 인문분야에서 특히 교육에 관한 분석연구에서 아직 도입을 거의 하지 않고 있다.
21세기 인공지능 시대에 들어 고전교육은 세계의 유명대학 뿐만 아니라 우리나라 대학에서도 기초필수 혹은 교양과목으로 지정되어 있다. 고전이란 라틴어의 클라시쿠스(classicus)에서 유래된 것으로 인간의 정신을 풍부하게 하고 영원성을 가지고 있으며 그 표현이 고매하며 보편성과 포용성을 가지고 있는 것으로 정의된다. 그리하여 고전수업은 인간의 사고력을 함양시키며, 논리적 사고력을 제고하고 삶의 가치관을 변화시킨다. 2023년 현재 다문화사회에 접어들기 시작한 우리나라의 대학들의 고전수업에서는 한국인 학생뿐만 아니라 외국인 유학생들도 상당히 많이 있다. 그러나 고전수업의 학습변인별로 학습효과를 분석한 실증적 연구는 극히 희소한 실정이다.
더구나 고전수업의 학습효과를 분석하기 위하여 대부분 기존연구들은 전통적인 통계분석 즉 상관분석 혹은 회귀분석 등에 의한 통계방법을 사용하였다. 그러나 이들 전통적 통계분석에 의한 실증적 연구들은 먼저 모형설정의 오류가 있으며, 과잉적합의 문제가 발생한다. 따라서 이러한 전통적 추정과 학습효과 예측의 한계점을 보완하기 위하여 최근 머신러닝과 딥러닝 등의 인공지능을 이용한 추정기법을 여러 타 학문분야의 실증분석에서 도입되고 있다.
그리하여 본 연구는 최근 머신러닝과 딥러닝 등의 AI 기법을 사용하여 고전수업의 학습효과를 분석하고자 한다. 최근 Kreif and DiazOrdaz (2019), Athey (2017, 2019)는 분석 자료와 정책의 문제 및 인공지능에 있어 머신러닝의 대한 충격에 대한 연구, Nielsen (2015), Gu et al. (2018, 2019), Agrawal et al. (2018), Athey and Imbens (2019) 등이 머신러닝 기법에서 소개하고 있듯이 정책효과를 분석에 있어 머신러닝과 딥러닝 등의 인공지능 기법을 사용하여 그 효과를 예측하는 것이 인공지능 기법을 사용하지 않는 전통적 통계분석보다 우월하다고 평가받고 있다. 그럼에도 불구하고 우리나라에서는 고전수업의 학습효과를 분석하고 예측하는데 있어 머신러닝이나 딥러닝 등의 기법에 의해 교육 분야의 효과분석은 전혀 없는 실정이다.
따라서 본 연구에서는 대학생을 대상으로 하는 고전수업에 있어 학습효과 등을 예측하고 비교 분석하기 위해 가설설정을 통한 전통적 회귀모형과 머신러닝 등의 인공지능 분석방법을 도입하여 고전수업의 학습효과를 좀 더 정확히 분석하고자 한다. 이를 위하여 비선형 머신러닝 모형들인 의사결정나무(Decision Tree), 서포트 벡터 머신(Support Vector Machine), 심층 신경망(Deep Neural Networks)을 이용한 딥러닝(Deep Learning) 모형 등을 사용하여 다음과 같이 연구분석을 하고자 한다.
첫째, 대학의 고전 교육에 있어 설문조사를 통하여 고전수업을 듣고 있는 학생들의 국적, 고전에 대한 인식변인 등을 통하여 학습변인에 따른 학습효과를 비교분석하고 최근 도입된 인공지능에 기반한 머신러닝과 딥러닝 등의 분석기법을 통하여 의사결정나무 모형과 서포트 벡터 머신모형 등에 따라 그 학습효과를 분석한다.
둘째, 현재 대학에서 전통적인 회귀분석 모형과 최근 도입되기 시작한 인공신경망 등의 머신러닝과 딥러닝 모형 기법을 통하여 주로 모형의 결정계수와 평균자승오차(MSE)를 중심으로 그 학습효과를 비교 분석한다.
셋째, 그리하여 대학교의 고전수업에 대한 다문화 학습자 고전수업에 대한 인식변인별로 고전수업의 학습효과를 여러 인공지능에 기반한 머신러닝과 딥러닝 기법을 도입하여 분석하여 고전수업에 대한 만족도를 조사하여 비교 분석한다. 마지막으로 본 연구결과를 통하여 우리나라 대학의 향후 고전 교육의 방향과 향후 고전 교육정책에 대한 시사점을 제시한다.
따라서 본 연구의 공헌점을 보면 다음과 같다. 현재까지 우리나라에서 고전수업에 대한 연구도 희소하지만, 대학생들을 대상으로 고전수업의 학습효과를 실증적으로 심층 분석하기 위한 실증 통계적 연구는 미약한 편이다. 더구나 인공지능에 기반한 머신러닝과 딥러닝을 통한 고전수업의 학습효과에 대한 실증연구는 우리나라에서 아직 전혀 없기 때문에, 연구주제 및 연구방법에 있어 독창성을 가지고 후발연구를 유발하는데 기여할 수 있을 것이다.
2. 이론적 배경과 선행 연구
2.1. 대학에서의 고전수업 배경과 학습변인
고전은 선인들의 보편적 지혜와 시대를 꿰뚫는 통찰력과 역사의식과 인생관을 확립하는데 도움을 준다. 대학은 고전을 통해서 학생들의 인생관을 변화시킬 수 있다. 또한 고전은 대학생들의 사고력을 사고력을 함양시켜, 논리력과 창의력 등을 제고하고 삶의 가치관을 변화시킨다.
그리하여 우리나라 대학들은 고전과 고전연관 과목을 많이 개설하고 있다. 그리고 최근에는 외국인 유학생들이 우리나라 대학에 많이 오고 있는데, 이들 외국인학생들과 다문화학생들을 대상으로 우리나라 대학은 다문화학생들을 위한 고전읽기 수업과 토론 등의 과목을 개설하고 있다.
그리고 우리나라 대학에서 중요한 과목으로 설정되고 있는 고전연관과목을 수강하고 있는 한국 및 외국 대학생들의 학습효과를 추정하는 것은 아주 중요하다. 그 학습변인으로는 학생의 국적과 성별 변인, 고전에 대한 흥미, 고전수업의 필요성과 중요성 등에 대한 인식변인, 그리고 학습에 도움을 주는 학습과정 등이 중요한 변인이 된다. 그리고 외국인 대학생들의 한국어 실력과 한국에 대한 이해 등이 그 학습효과에 크게 영향을 미칠 수 있다. 이와 같이 고전수업 만족도에 영향을 주는 중요한 학습변인을 살펴보면 크게 다음과 같이 나눌 수 있다.
첫째, 가장 기본적인 다문화 유학생들의 문화적 배경으로 한 다문화 대학생들의 학습변인으로 국적, 성별, 출신국가, 한국어 실력과 한국문화에 대한 이해력 등이 있다.
둘째, 한국인 학생과 외국인 학생들로 이루어진 다문화 대학생이 생각하는 고전수업의 필요성, 고전수업에 대한 흥미도, 고전에 대한 중요성, 상호문화 이해력 등 다문화 학습자들의 인식변인 들을 비교 조사한다.
셋째, 학습과정 변인으로 다문화 대학생들의 다문화 고전수업 이해와 토론을 바탕으로 영화감상을 통한 고전이해의 도움, 다문화 의사소통과 토론수업을 통한 다문화적 표현력과 발표력 신장, 논리적 사고력 향상 등이 있다.
2.2. 선행연구
최근 머신러닝에 대한 외국의 연구를 보면, Kreif and DiazOrdaz (2019), Athey (2017, 2019), Agrawal et al. (2018)와 Athey and Imbens (2019) 등이 좀 더 나은 예측과 정책효과 분석을 위해 머신러닝 기법을 도입하고 있지만, 아직 우리나라에서 학습효과 분야에서는 머신러닝 모형을 활용한 연구가 전혀 없는 실정이다.
우리나라에서도 물론 수업효과에 대한 전통적인 통계분석에 의한 기존 실증연구는 있지만 아직 많이 미흡한 실정이다. 김종영(2008)은 고전을 의사소통 교과목 수업으로 주로 모형개발을 연구하였다. 정인모(2007)는 교양교육으로서 고전과목에 대한 연구를 하였다. 이황직(2011)은 고전을 통한 교육의 혁신에 대한 연구를 주로 하였다. 전은진(2014)은 고전읽기의 교육적 효과를 연구하였고, 김민라(2015)는 외국인 학습자를 위한 고전수업 연구를 하였다.
강옥희(2016)와 박현희(2019)는 독서와 고전읽기 수업의 효율적 운영에 대한 연구를 하였다. 김수진(2020)은 고전 독서와 고전소설 교육방안에 대한 연구를 하였다. 유경애(2018, 2022)는 다문화 학생들에 대한 고전수업의 학습효과를 분석하였고, 다문화적 학습변인들과의 관계를 실증분석하였다.
그러나 위의 기존연구들은 고전에 대한 연구들 모두 최근 도입된 머신러닝과 딥러닝 기법에 의한 분석은 하지 않았다. 더구나 기존 선행 연구들은 대부분 우리나라 학생들을 대상으로 독서와 읽기 중심으로 고전수업에 대한 연구를 하고 있다. 따라서 주로 대학의 독서토론 교육, 의사소통, 그리고 교양교육의 일환으로 주로 고전수업의 활성화를 위한 연구가 주종을 이루고 있다.
그리하여 본 연구는 아직 우리나라에서 고전학습 분야에서 도입하고 있지 않는 인공지능에 기반한 머신러닝과 딥러닝 기법에 의한 고전읽기와 토론 학습의 효과를 예측하는 분석을 함으로써 학문적으로 볼 때, 새로운 연구방법과 연구해석 등을 제시하고 아울러 우리나라 고전읽기 수업에 대한 시사점을 제공해줄 수 있다.
3. 머신러닝과 딥러닝 연구모형
본 연구는 우리나라의 대학에서 고전수업을 수강하고 있는 한국인 학생과 외국인 학생들로 구성된 대학생들을 중심으로 설문조사 등을 통해 고전수업의 만족도와 학습효과에 대한 전통적인 회귀분석은 물론이고, 최신기법인 머신러닝과 딥러닝 기법 등을 이용하여 실증적으로 분석한다.
3.1. 연구설계와 머신러닝과 딥러닝 기법
본 연구의 연구조사 대상과 방법은 먼저 우리나라 부산지역 대학교에서 수업을 듣고 있는 한국인과 외국인 유학생들의 고전수업 수강생 대상으로 연구조사를 실시한다. 전통적 통계방식뿐만 아니라 머신러닝이나 딥러닝 등의 최신 인공지능 기법에 의한 학습효과 추정에 대한 실증분석을 할 것이다.
그리고 설문 작성과 표본의 신뢰도 증진을 위해서 직접 대학교에서 수강하는 있는 대학생들을 대상으로 표본을 설정한다. 그리하여 표본설정에 따른 신뢰성 문제를 극복하기 위하여, 현재 수업을 듣고 있거나 수업을 들었던 9개 분반의 학생들을 중심으로 우리나라 대학생들과 외국인 대학생으로 구성된 266명을 대상으로 분석한다.
마지막으로 고전수업의 만족도에 대한 학습효과를 추정하기 위해, 학습변인들로 분석하기 위하여 전통적 통계분석이 아니라, 최근 도입하고 있는 인공지능에 기반한 의사결정 나무, 서포트 벡터 머신, 인공신경망이 좀 더 진전된 딥러닝 모형 등을 도입하여 고전수업의 학습효과를 좀 더 엄밀히 추정하고 예측한다.
3.2. 의사결정 나무(Decision Tree) 모형
의사결정 나무는 계층적 구조로 이루어진 것을 나무형태로 도표화하여 예측하는 모형이다. 그리하여 최적의 분할변수와 분할점을 선택하는 것으로 회귀트리의 경우 잔차제곱합을, 분류트리는 엔트로피 등의 불순도를 최소로 한다. 그리고 불순도의 측정지수는 지니 지수(Gini Index)와 엔트로피 지수(Entrophy Index)를 도입하여 사용한다.
그리하여 노드 m, 영역 Rm, 그리고Nm개의 관측치가 있을 때, 노드 m에서 k 클래스의 관측치들의 비율을
3.3. 서포트 벡터 머신(Support Vector Machine) 모형
서포트 벡터 머신(SVM) 모형은 최대 마진 초평면을 구하는 문제에 커널 트릭을 적용하는 비선형 분류방법을 사용하는 것으로 고차원 공간으로의 데이터 이동이 가능하게 하여 한다. 그리고 고차원 공간으로의 이동을 위해 커널 함수(Kernel Function)를 이용하여 커널 함수를 통해 비선형적으로 매핑하여 선형적으로 분리를 가능하도록 다음과 같은 절차를 거쳐한다. 첫째, 아래의 식을 이용해서 α를 SMO(Sequential Minimum Optimization) 알고리즘인 텐셔플로 최적화(Tensorflow Optimizer)를 다음과 같은 Dual 원리를 사용하여 찾는다.
둘째, α>0인 점의 조합을 하나 선택해서, 아래와 같은 분류기(Classifier)를 만든다.
여기서 사용될 Kernel은 보통 다항식 Kernel과 방사기저함수 (radial basis function, RBF)등을 선택한다.
3.4. 심층 신경망과 딥러닝(Deep Learning) 모형
심층신경망은 입력층과 출력층 사이에 다수의 은닉층(hidden layer)을 가지고 있는 인공 신경망 모형을 좀 더 개발한 딥러닝(Deep Learning)의 핵심 모델이므로 다양한 비선형적 관계를 학습할 수 있다. 그리하여 본 연구에서는 다층 퍼셉트론(Multi-layer Perceptron; MLP) 모형이 구현되는 MLP 함수를 이용한다. MLP 함수에서는 모형의 복잡도의 규제항인 알파(alpha)를 적정하게 찾아낸다.
Nielsen (2015)은 인공 신경망의 문제점이었던 과잉적합 문제를 경사도(gradient)의 소멸 등의 새로운 초기화 방법을 통해 해결하였다. 심층 신경망은 피드포워드(Feed forword) 신경망으로 구성되어 있으며, 역전파(back propagation) 알고리즘을 통해 각 노드의 가중치를 갱신하여 모형을 최적화한다.
따라서 본 연구는 고전수업의 학습효과를 분석하기 위하여 전통적 회귀모형과 인공지능을 기반으로 하는 머신러닝 연구기법에 따라 고전수업의 학습변인별 고전수업의 효과성을 분석하고 학습변인별 학습효과를 추정하여 비교분석한다.
4. 학습만족도에 대한 실증분석
4.1. 전통적 회귀분석과 학습효과
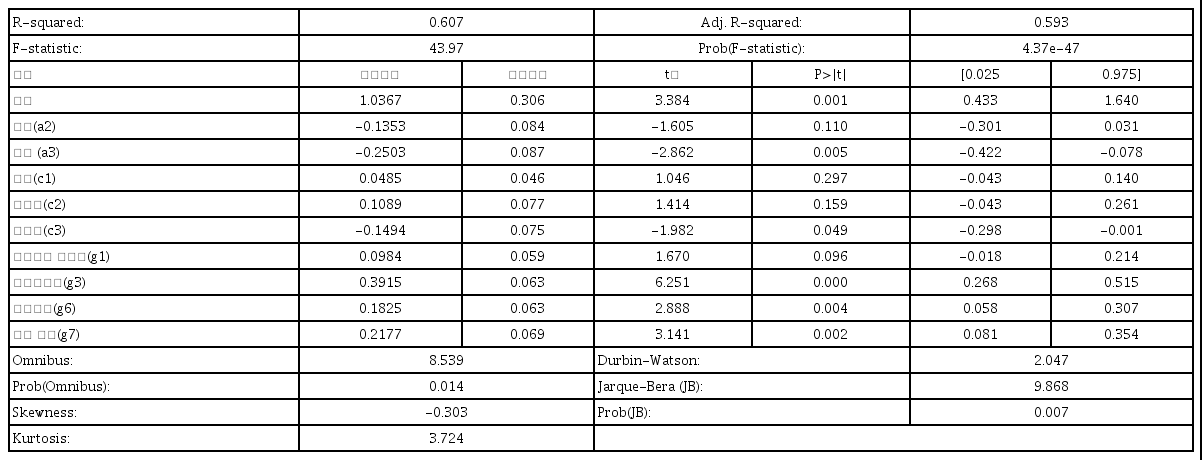
본 절에서는 전통적인 최소자승법(OLS)에 의한 선형회귀모형을 설정하여 고전수업효과를 추정한다. 그리하여 종속변수인 고전수업에 대한 학습만족도(h2)에 대한 예측과 추정을 한다. 고전수업의 만족도에 대한 효과를 분석하기 위하여, 9개 학습변인들 즉 학생들의 성별(a2), 국적(a3), 고전 흥미(c1), 고전 중요성(c2), 고전 필요성(c3), 표현력과 발표력 신장(g1), 가치관 형성(g3), 영화감상의 고전수업 유익(g6), 토론의 고전이해에 대한 유익(g7) 등을 독립변수로 삼고 분석할 것이다.
그리하여 추정한 결과가 <표 1>에 나타나 있다. 먼저 모형의 설명력을 보면 회귀모형의 조정된 결정계수는 0.593으로 비교적 높은 것으로 나타났다. 그리고 모형의 유효성을 보면 F 통계량은 높고 그 확률값은 0.05보다 낮아, 고전수업의 만족도에 대한 추정모형이 5% 유의수준에서 유효한 것으로 나타났다. Durbin-Watson 통계량은 2.047로 나타났으므로 자기 상관성(autocorrelatin) 문제는 발생하지 않는다. 그러나 Omnibus는 8.539로 나타났고 그 확률값인 Prob(Omnibus)는 0.014로 나타났으며, Jarque-Bera (JB)는 9.869로 나타났지만 그 확률값인 Prob(JB)는 0.007로 나타났다. 그리하여 5% 유의수준에서 정규분포하고 있다는 귀무가설을 모두 기각하고 있는 것으로 나타났다. 마지막으로 좌측으로 조금 왜도(skewness)가 나타났고, 첨도(Kurtosis) 역시 3.0보다 다소 높아 역시 정규분포하고는 조금 다르게 나타났다.
그리고 수업의 만족도에 대한 추정결과는 <표 1>에 나타난 것과 같이, 학습자 변인 중 학생들의 성별은 유의한 영향을 미치지 않으나 학생들이 한국인이 아니고 외국인은 만족도에 부의 영향을 미치고 있다. 이것은 한국인 학생보다 외국인 학생들이 한국어가 미숙하여 수업을 잘 이해하지 못하여 만족도(h2)가 낮은 것으로 나왔다.
한편, 학습의 인식변인으로 고전읽기에 대한 흥미(c1), 고전읽기에 대한 중요성(c2) 등은 수업의 만족도에 유의하게 영향을 미치지 않는 것으로 나타났다. 그러나 고전의 필요성(c3)에 대한 인식은 5% 유의수준에서 외국인 학생들이 수업이 더 필요하고 중요하다고 생각했던 외국인 학생들이 외국인 학생들이 한국어로 시행되는 고전수업에 대한 만족도가 더 떨어진 것으로 나타났다.
고전수업을 통하여 표현력과 발표력 신장(g1)을 기대하는 것은 5% 유의수준에서 영향을 미치지 않는 것으로 나타났지만 10% 유의수준에서는 수업의 만족도에 영향을 미치는 것으로 나타났다. 그러나 가치관 형성의 도움(g3), 영화감상의 고전읽기 도움(g6), 토론의 고전이해에 대한 도움(g7) 등 3개의 학습변인들은 5% 유의수준에서 모두 고전수업의 만족도에 긍정적인 영향을 미치고 있는 것으로 나타났다.
4.2. 의사결정나무 모형에 의한 분류와 고전수업 만족도 분석
4.2.1. 의사결정나무 머신러닝 모형에 의한 분류예측
의사결정나무의 훈련 알고리즘의 목적은 기본적으로 회귀나무의 경우 MSE 값을, 분류는 불순도를 최소로 해야한다. 엔트로피가 클수록 불순도가 높아진다. 지니 지수는 0과 1사이의 값을 가지는데, 지니 지수는 낮을수록 순수도는 높게 측정된다. 데이터는 학습용은 70%(0.7), 평가용은 30%(0.3)으로 나누었고 random_states는 0으로 두었다.
① 의사결정나무에 의한 분류예측 모형의 평가와 정확성
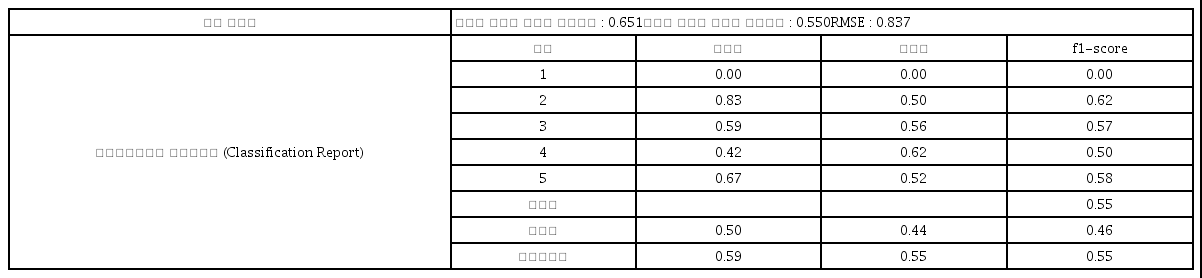
<표 2>에서는 9개의 독립변수로 사용하여 의사결정나무 모형에 의한 분류예측 모형의 성능과 정확성을 평가하기 위하여 결정계수와 RMSE를 구하였다. 그리하여 추정결과, 학습용 데이터의 결정계수는 비교적 높은 0.651, 평가용 데이터의 결정계수는 0.550로 나타났으며, RMSE는 0.837로 나타나 의사결정나무 모형의 정확성은 비교적 있는 모형으로 나타났다.
그리고 의사결정나무 모형에 의한 고전수업의 만족도에 대한 분류예측 모형의 성능 평가를 보면, 정밀도는 클래스 2가 0.83으로 가장 높게 나타났고, 클래스 3은 0.59, 그리고 클래스 4와 클래스 5에 대서는 각각 0.42와 0.67로 비교적 높게 나왔지만 클래스 1은 0으로 나왔다. 재현율에 대해서는 클래스 1을 제외하고는 0.50-0.62로 비교적 높게 나왔다. 그리고 f1-스코어 값 역시 클래스 2는 0.62, 클래스 3은 0.57, 클래스 4는 0.50, 그리고 클래스 6에서는 0.58로 각각 나타났다. 정확도는 약 55%, 평균과 가중평균도 0.46과 0.55로 비교적 좋은 모형으로 나타났다.
② 분류예측 모형 변수의 중요도
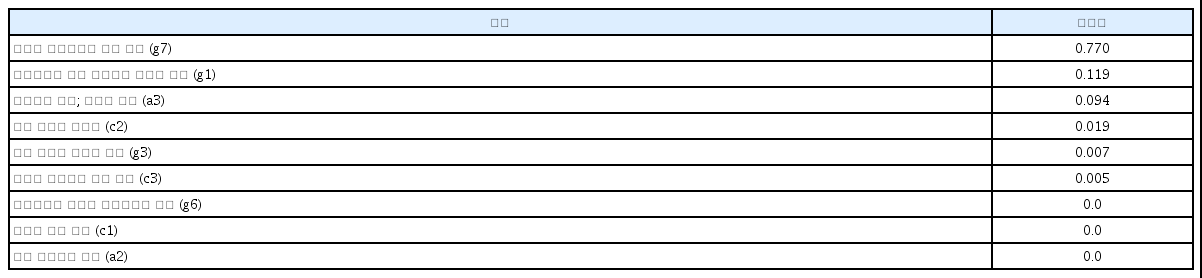
의사결정나무는 투입된 독립변수들에 대한 특징(feature)을 나타내는변수 선택을 자동적으로 수행한다. 본 절에서는 과연 몇 개의 중요한 독립변수들이 선택되었는가를 살펴본다. 그리하여 사용된 독립변수들의 중요성을 <표 3>에서 보면, 고전수업이 고전을 이해하는데 도움(g7)이 중요성이 0.769로 제일 높게 나타났고, 그 다음에는 고전수업의 표현력과 발표력에 대한 도움(g1)의 중요성이 0.119로 높게 나타났다.
그 다음에는 수업을 듣고 있는 대학생들의 국적 즉 한국인과 외국인의 차이(a3)의 중요성이 0.094로 나타났고, 그 다음에는 평소 고전읽기의 중요성(c2)이 0.019로 나타났다. 그 외 영화감상을 통한 수업의 도움(g6), 삶의 가치관 형성(g3), 평소 고전의 필요성(c3), 고전읽기에 대한 흥미(c1), 그리고 남녀 성별의 중요성(a2)은 유의하게 나타나지 않았다.
4.2.2. 의사결정나무 모형과 수업 만족도 회귀예측
① 의사결정나무에 의한 회귀모형의 평가와 정확성
본 절에는 9개의 독립변수로 사용하여 종속변수인 고전수업의 학습효과를 예측하는 의사결정나무 모형을 만들어 회귀분석하기 위해, 의사결정나무의 사전 가지치기 옵션을 사용하였다. 나무의 최대 깊이(Max Depth)를 5로 두었을 때는 그림이 너무 복잡하여 나무 깊이를 3으로 설정하였다. 그리고 <표 4>에서 나타난 것처럼, 의사결정나무 모형의 성능을 평가하기 위해서 그 결정계수와 MSE를 구한다. 그 추정결과 학습용 데이터 세트의 결정계수는 0.596, 평가용 데이터 세트의 결정계수는 0.437로 각각 나타났다. 그리고, MSE도 0.807로 나타나, 의사결정 모형은 비교적 좋은 모형을 나타내고 있다.
② 의사결정나무 모형의 변수 중요도
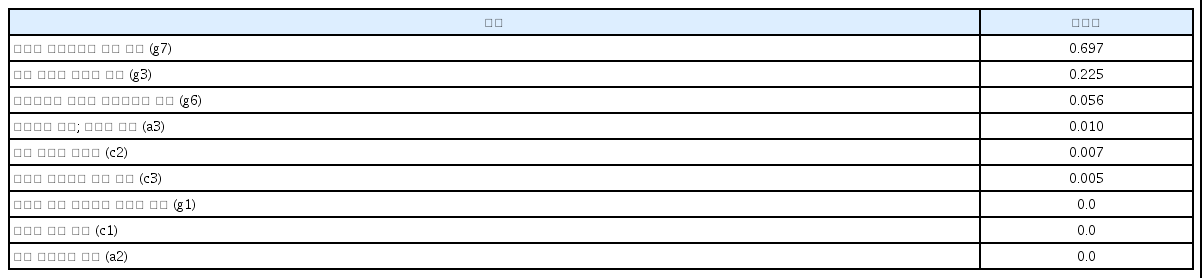
의사결정나무는 투입된 독립변수들에 대한 변수 선택을 자동적으로 수행한다. 본 절에서는 과연 몇 개의 중요한 독립변수들이 선택되었는가를 살펴본다. 그리하여 사용된 독립변수들의 중요성을 <표 5>에서 보면, 고전수업이 고전을 이해하는데 도움(g7)이 중요성이 0.697로 제일 높게 나타났고, 그 다음에는 고전수업의 삶의 가치관 형성에 도움(g3)이 0.226으로 상당히 높게 나타났다.
그리고 영화감상이 고전을 이해하는데 도움여부(g6)가 0.056, 그 다음에는 수업을 듣고 있는 대학생들의 국적 즉 한국인과 외국인의 차이(a3)의 중요성이 0.010의 순으로 높게 나타났다. 그 다음에는 평소 고전읽기의 중요성(c2)이 0.007, 평소 고전의 필요성(c3)이 0.005로 나타났다. 그러나 표현력과 발표력 향상(g1), 고전읽기에 대한 흥미(c1), 그리고 남녀 성별의 중요성(a2)은 나타나지 않았다.
③ 의사결정나무에 의한 고전 학습효과에 대한 회귀예측
[그림 1]에서와 나타나 있듯이 의사결정나무에서 보면, 각 노드상에 나타난 값(value)은 각 클래스 혹은 값이 나타내는 빈도수를 나타내며 이를 통해 해당 데이터에 대한 예측을 어떻게 수행했는가를 나타낸다, 수업 만족도에 대한 수치는 아주 높음 5, 조금 높음 4, 보통 3, 조금 낮음 2, 아주 낮음 1등으로 표시되어 5개로 표시되어 있지만, 5개의 클래스로 나누지는 않았다. 그리고 앞에서와 같이 의사결정나무의 최대 깊이는 3으로 설정하였다.
[그림 1]에서 고전수업이 고전을 이해하는데 도움(g7)이 2.5이하일 때 참(True)이면 왼쪽에 있는 노드로 내려가고, 그 값이 2.5보다 크면 거짓(False)이므로 오른쪽에 있는 노드로 내려간다. 그리하여 오른쪽 노드에서 다시 고전수업의 삶의 가치관 형성에 도움(g3)이 4.5이하이면 참이므로 왼쪽 노드로 가고, 그 값이 4.5보다 크면 거짓이므로 오른쪽 노드로 내려간다. 참인 오른쪽 노드에서 다시 영화감상이 고전을 이해하는데 도움(g6)이 4.5보다 큰 것으로 나타나면 고전수업에 대한 만족도가 아주 높은 4.808로 예측되고, 반면 영화감상이 고전을 이해하는데 도움여부(g6)가 4.5이하인 것으로 나타나면 고전수업에 대한 만족도가 다소 높은 4.13으로 예측된다.
한편, 고전수업의 삶의 가치관 형성에 도움(g3)이 4.5이하이면 참이므로 왼쪽노드로 내려간다. 여기서 만약 고전수업이 고전을 이해하는데 도움(g7)이 3.5이하이면 참이므로 만족도가 3.324로 다소 높게 나타났고, 그 값(g7)이 3.5보다 높게 나타나면 고전수업에 대한 만족도가 이 보다 더 높은 3.988로 나타났다.
반대로 고전수업이 고전을 이해하는데 도움(g7)이 2.5이하일 때 참(True)이면 왼쪽 노드로 내려가고, 여기서 만약 학생들이 한국인(a3)이면 참이므로 다시 왼쪽 노드로 내려간다. 평소 고전의 필요성(c3)이 좀 낮은 2.5이하로 내려가면, 그것이 참일 때는 다시 왼쪽노드로 내려가서 고전수업에 대한 만족도가 좀 낮은 2.000로 예측되고, 반면 평소 고전의 필요성(c3)이 2.5보다 크게 나타나면, 고전수업에 대한 만족도가 매우 낮은 1.000로 예측되어 진다.
위에서 만약 의사결정나무에서 고전수업이 고전을 이해하는데 도움(g7)이 2.5이하일 때 참(True)이므로 왼쪽 노드로 내려가고, 거기서 학생들이 외국인이면 a3가 1.5보다 크게 나타나 거짓이므로 다시 오른쪽 노드로 내려간다. 여기서 만약 외국인 학생들이 평소 고전읽기의 중요성(c2)을 낮게 평가하여 1.5이하 이면 별로 수업에 대한 기대를 하지 않아서 왼쪽노드로 내려가서 수업의 만족도(만족도=2)가 보통인 3.0으로 나타나고, 평소 고전읽기의 중요성(c2)이 1.5보다 높게 외국인 학생들이 생각했다면, 한국어와 한국어 교재로 이루어진 고전수업에 대한 어려움으로 만족도(만족도=2)가 낮게 예측되어 나타난다.
여기서도 고전을 이해하는데 도움여부에 의해 첫마디가 나누어지므로 위에서와 같이 고전수업에 있어서의 만족도에 상당히 중요한 조건이 되는 것으로 다시 한 번 확인된다. 그리고 의사결정나무 모형에 의한 수업만족도의 수치예측에서 각 노드의 선행조건들 즉 고전수업의 삶의 가치관 형성에 도움(g3)이 0.226으로 상당히 높게 나타났다. 그리고 영화감상이 고전을 이해하는데 도움여부(g6), 대학생들의 국적 즉 한국인과 외국인의 차이(a3)의 중요성, 평소 고전읽기의 중요성(c2), 그리고 평소 고전의 필요성(c3) 등에 의해 고전수업의 만족도가 다르게 나타나고 있는 것을 알 수 있다.
4.3. 서포트 벡터 머신(SVM) 모형과 수업 만족도 분석
서포트 벡터 머신 모형을 최적화하기 위해서는 커널 함수, 오류 마진을 제어하는 인자인 C, 데이터의 영향력에 관계된γ (gamma), 그리고 평가 데이터의 허용 오차율과 관련된 ε(epsilon)에 대한 옵션들의 선택을 해야 한다. 본 연구에서는 서포트 벡터 머신 모형 커널 함수로 RBF 커널을 적용하여, k겹 교차검증에 의해 산출된 검증(validation) 데이터의 RMSE가 최소가 되는 모형을 택한다.
4.3.1. 서포트 벡터 머신모형에 의한 분류예측
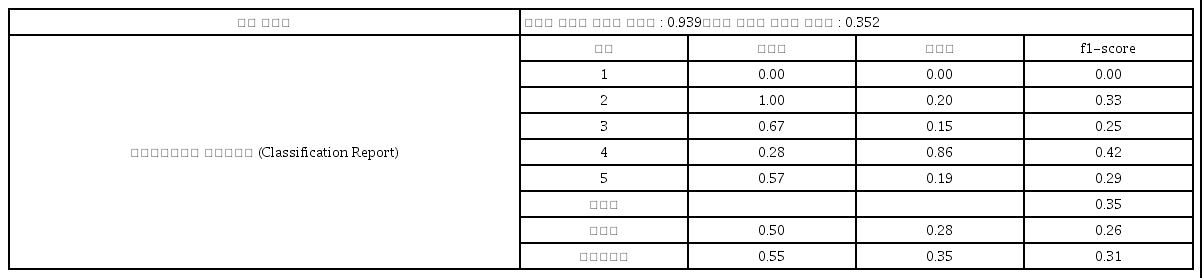
서포트 벡터 머신 모형에 의한 분류예측을 하기 위해서 모형의 하이퍼 패러미터(hyperparameter) 혹은 인자로서 오류의 범위와 연관이 있는 모형의 패러미터인 C=1000, gamma=10, random state=0으로 두었을 때, <표 6>에서 나타나 있듯이, 모형의 학습용 데이터 세트는 0.939로 아주 높게 나왔지만, 평가용 데이터 세트의 결정계수는 0.352로 아주 낮게 나왔다. 그리하여 서포트 벡터 머신 모형에 대한 분류예측에서는 과잉적합의 문제가 발생할 가능성이 아주 높게 나타나고 있다.
그리고 서포트 벡터 머신 모형에 의한 분류예측을 위한 고전수업의 만족도에 대한 분류예측 모형의 성능 평가를 보면, 정밀도는 클래스 1과 클래스 3, 그리고 클래스 5에 대서는 각각 1.00, 0.67, 그리고 0.57 등으로 비교적 높게 나왔지만 그 외 클래스에 대해서는 낮게 나타내고 있다. 재현율에 대해서는 클래스 2는 0.20 나타났으며, 클래스 4는 아주 높게 0.89로 나타났지만, 클래스 6은 0.19로 낮게 나타났다.
그리고 f1-스코어 값이 클래스 2는 0.33, 클래스 4는 0.42, 그리고 클래스 6에서는 0.29로 각각 나타났다. 정확도는 약 35%로 정도로 비교적 낮게 나타났고 평균과 가중평균도 0.26과 0.31로 낮게 나타났다. 그리하여 SVM 모형에 의한 고전수업의 만족도에 대한 분류예측의 정확도는 비교적 높게 나타나지 않았다.
4.3.2. 서포트 벡터 머신모형에 의한 회귀예측
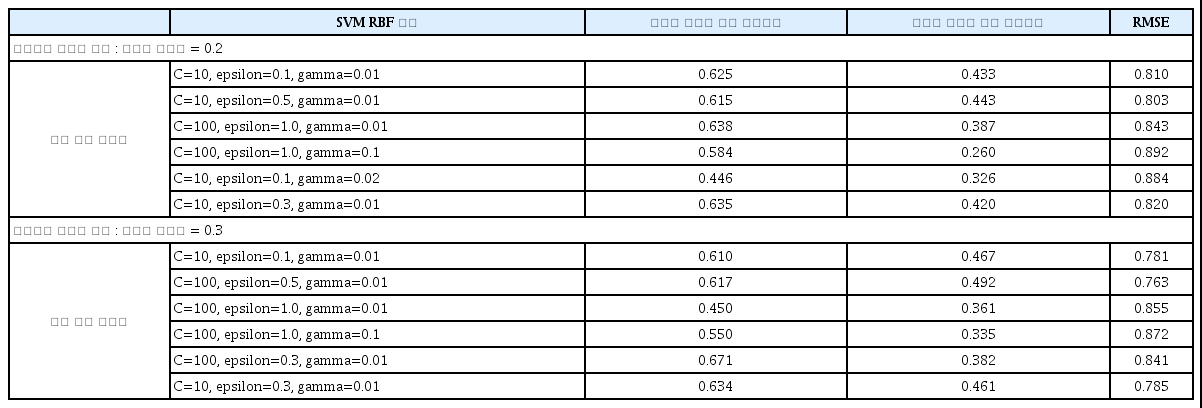
본 절에서 서포트 벡터 머신 회귀모형(SVR) 분석을 하는데, 이러한 서포트 벡터 머신 회귀분석과 모형평가에 대한 추정결과가 <표 7>에서 모형 데이터의 결정계수와 RMSE가 나타나 있다. 그리고 이 회귀모형에 대한 오류의 범위와 연관이 있는 인자 C를 10, 100, 1000 등으로 변동시켜 그 변동을 본다. 또한 서포트 벡터 머신 회귀모형의 인자인 epsilon값을 0.1부터 1까지 조금씩 변동을 시키고, RBF 함수의 커널 계수를 나타내는 gamma 값을 0.01에서 0.1까지 변동시켜 본다. 그리하여 그 결정계수들과 RMSE를 구하였는데 그 추정결과를 차례로 보면 다음과 같다.
첫째, 먼저 학습용 데이터 세트 80%와 평가용 데이터 세트를 20%로 나누었을 때, 9개의 독립변수들이 고전수업의 만족도에 미치는 영향을 서포트 벡터 머신 회귀 모형으로 예측한 결과를 <표 7>의 상단에서 보면 다음과 같다. 서포트 벡터 머신 회귀모형의 인자들이 각각 C=10, epsilon= 0.1, gamma=0.01 일 때, 학습용 데이터 세트의 결정계수는 0.625, 평가용의 데이터 세트의 결정계수는 0.433으로 나타났고, RMSE는 0.810으로 도출되어 나왔다. 그 다음 모형의 인자들이 각각 C=10, epsilon=0.5, gamma=0.01일 때 두 개의 결정계수들이 각각 0.815와 0.443, 그리고 RMSE는 0.833 등으로 나와 예측력이 비슷하게 무난한 모형으로 나왔지만, 학습용 데이터 세트의 결정계수는 아주 조금 낮아졌고 평가용 데이터 세트의 결정계수는 아주 조금 높아졌다.
한편, 마진과 관계있는 C를 100으로 증가시켜, C=100, epsilon=1.0, gamma=0.01 일 때, 학습용 데이터 세트의 결정계수는 조금 높아진 반면, 평가용 데이터 세트의 결정계수는 조금 낮아졌고, RMSE는 조금 높아진 0.843으로 높아졌다. 그리고 C=100, epsilon=1.0, gamma=0.1 일 때는 앞의 경우보다 학습용과 평가용 데이터 세트의 결정계수들은 모두 낮아져 좋은 모형으로 나오지 않았고, RMSE 역시 0.892로 나타나 예측오차가 더 크게 나타났다.
그래서 다시 마진과 연계된 인자인 C를 줄이고 gamma를 조금 높여서, C=10, epsilon=1.0, gamma=0.02일 때 도출해보니 학습용과 평가용 데이터 세트의 결정계수들은 gamma=0.01일 때 보다 모두 낮아졌고, RMSE는 조금 더 높아진 0.884로 나타나 예측오차가 더 크게 나타났다. 그리하여 gamma=0.02일 때는 앞의 gamma=0.01 일 때보다 나쁜 모형으로 나타났다.
그러나 마지막으로 마진과 연계된 C는 그대로 10으로 두고 epsilon을 조금 상승시킨 결과, C=10, epsilon=0.3, gamma=0.1 일 때는 학습용 데이터 세트의 결정계수는 0.635, 평가용의 데이터 세트의 결정계수는 0.420으로 나타났고, RMSE는 0.820으로 도출되어 나왔다.
둘째, 학습용 데이터 세트 80%와 평가용 데이터 세트를 30%로 나누었을 때, 9개의 독립변수들이 고전수업의 만족도에 미치는 영향을 서포트 벡터 머신 회귀 모형으로 예측한 결과를 <표 7>의 하단에서 보면 다음과 같다.
서포트 벡터 머신 회귀모형의 인자들이 각각 C=10, epsilon=0.1, gamma=0.01 일 때, 학습용 데이터 세트의 결정계수는 0.610, 평가용의 데이터 세트의 결정계수는 0.467로 나타났고, RMSE는 0.781로 나왔다. 그 다음 모형의 인자들이 각각 C=100, epsilon=0.5, gamma=0.01일 때 두 개의 결정계수들이 각각 0.617과 0.492, 그리고 RMSE는 0.763 등으로 좀 더 나은 모형으로 나왔으며 예측력도 높아졌다.
그러나 epsilon=1.0으로 좀 더 높여, C=100, epsilon=1.0, gamma=0.01일 때와 C=100, epsilon=1.0, gamma=0.1 일 때 도출해보니, 학습용 데이터 세트의 결정계수와 평가용 데이터 세트의 결정계수 모두 낮아졌고, RMSE는 조금 높아져 좋은 모형으로 도출되지 않았다.
그리하여 epsilon을 더 줄여 0.3으로 하였을 때, C=100, epsilon=0.3, gamma=0.01일 때는 학습용 데이터 세트의 결정계수는 0.671로 제법 높아진 반면, 평가용의 데이터 세트의 결정계수는 0.382로 다소 낮게 나타났고, RMSE는 0.841로 나왔다. 마지막으로 마진과 연계된 C를 감소시켜, C=10, epsilon=0.3, gamma=0.01일 때는 학습용 데이터 세트의 결정계수는 0.634로 낮아진 반면, 평가용의 데이터 세트의 결정계수는 0.461로 나타났고, RMSE는 0.785로 무난한 모형으로 도출되었다.
그러므로 서포트 벡터 머신 모형에 의한 예측은 모형의 특징을 나타내는 모형의 인자들의 조합과 선택이 중요하며 그 인자인 인자들의 조합에 따라 값이 달라질 수 있다. 그리하여 위에서 보면 먼저 9개의 독립변수들을 가지고 고전수업의 만족도에 미치는 영향을 서포트 벡터 머신 회귀 모형으로 예측한 결과, 평가용 데이터 세트를 20% 혹은 30%로 나누었을 때 모두, 서포트 벡터 머신 회귀모형의 인자들이 각각 C=10, epsilon=0.1 혹은 0.3과 0.5, gamma=0.01 일 때 학습용과 평가용 데이트 세트의 결정계수와 RMSE로 볼 때 모두 무난하게 좋은 예측 모형으로 나타났다.
4.4. 딥러닝 모형에 의한 수업 만족도 분석
딥러닝의 심층신경망(DNN) 모형을 생성하고 학습 및 평가를 수행하기 위해서는 먼저 Keras 모듈의 순차적(Sequential) 함수를 도입한 후, 밀도(Dense) 함수와 활성화(Activation) 함수를 찾아낸다..딥러닝 모형의 주요한 인자들 중에서 전체 데이터에 의거한 학습의 반복 횟수(epochs; 에포크)와 학습되는 데이터의 개수(batch_size) 등을 사용한다.
4.4.1. 딥러닝 모형에 의한 분류예측
딥러닝의 심층 신경망 모형에 의한 고전수업의 만족도에 대한 분류예측을 위해 먼저 9개의 독립변수들을 설정한 후, 학습만족도를 종속변수로 삼고 추정예측을 하였다. 이를 위해 딥러닝 모형의 분류예측에서는 횡단 엔트로피를 설정하고, 경사하강법은 아담모형을 사용하였다. 그리고 순차적 함수를 이용하여 순차적 계층모형을 생성하고 추가하였다.
각층의 구조는 밀도 함수를 통해 결정되며 중요한 인자로서 활성화 함수로 은닉층에는 Relu 함수를 사용하였고, 출력층에는 Sigmoid 함수를 사용하였다. 그리하여 <표 8>의 첫째 행에서 나타난 것과 같이, 재학습을 통한 학습용 데이터 세트의 MSE는 0.418, 평가용 데이터 세트 MSE는 0.815로 각각 나타났다.
4.4.2. 딥러닝 모형에 의한 회귀예측
딥러닝 모형의 회귀를 통한 수치예측에서는 가중치의 업데이트를 위해서, 관성의 방향을 고려한 경사하강법인 모멘텀과 아다그라드(Adagrad)의 보폭 민감도를 보완하는 RMSProp 방식을 결합한 아담(Adam)을 사용하였다. 밀도(Dense) 함수의 활성화는 렐루(Relu) 함수를 사용하였다.
그리하여 <표 8>의 둘째 행 이하에서 나타난 것과 같이, 첫째, 고전수업의 만족도에 대한 딥러닝 회귀모형에 의한 수치예측을 살펴보면 다음과 같다. 그리하여 먼저 에포크(epochs)=20, 배치 크기(batch_size)= 64일 때 구한 학습용 데이터 세트의 MSE는 0.418,로 나타났고, 평가용 MSE는 0.815로 각각 나타났다.
둘째, 에포크와 배치 크기에 따른 MSE를 보면, 에포크= 40, 배치 크기= 64일 때 구한 학습용 데이터 세트의 MSE = 0.355, 평가용 MSE = 0.693로 각각 예측오차가 작은 것으로 나타나 앞의 고전수업의 만족도에 대한 딥러닝 모형보다 더 좋은 것으로 나타났다.
셋째, 에포크 수를 늘려 에포크=50, 배치 크기= 64일 때 구한 학습용 데이터 세트의 MSE = 0.339, 평가용 MSE = 0.676로 각각 예측오차가 작은 것으로 나타나 앞의 두 경우의 고전수업의 만족도에 대한 딥러닝 모형보다 더 좋은 것으로 나타났다.
셋째, 에포크 수를 늘려 에포크=50, 배치 크기= 64일 때 구한 학습용 데이터 세트의 MSE = 0.339, 평가용 MSE = 0.676로 각각 예측오차가 작은 것으로 나타나 앞의 두 경우의 고전수업의 만족도에 대한 딥러닝 모형보다 더 좋은 것으로 나타났다.
넷째, 에포크 수를 더 늘려 에포크=60, 배치 크기= 64일 때 구한 학습용 데이터 세트의 MSE = 0.328, 평가용 MSE = 0.652로 각각 예측오차가 앞의 경우보다 더 작은 것으로 나타나 앞의 세 경우의 고전수업의 만족도에 대한 딥러닝 모형보다 더 좋은 것으로 나타났다.
다섯째, 에포크 수를 더욱 더 늘려 에포크=100, 배치 크기= 64일 때 구한 학습용 데이터 세트의 MSE = 0.328, 평가용 MSE = 0.652로 각각 예측오차가 앞의 경우보다 더 작은 것으로 나타나 앞의 세 경우의 고전수업의 만족도에 대한 딥러닝 모형보다 더 좋은 것으로 나타났다.
마지막으로 에포크와 배치 크기를 동시에 증가시켜, 에포크=100, 배치 크기= 100일 때 구한 학습용 데이터 세트의 MSE = 0.317, 학습용 데이터 세트MSE = 0.627로 각각 가장 작게 나타나, 위의 다른 에포크와 배치 사이즈 조합들보다 에포크와 배치 크기가 (100, 100)일 때 학습용 데이터 세트와 평가용 데이트 세트의 MSE가 가장 작게 나타나서 가장 좋은 예측 모형으로 나타났다.
그리하여 종합적으로 머신러닝과 딥러닝 모형의 결과에서 보면, 고전수업의 만족도에 대한 영향을 예측할 때, 서포트 벡터 머신 모형과 딥러닝 모형에서는 모형 인자들의 조합과 선택이 중요하며, 그 선택결과에 의해 모형의 주청 결과가 조금씩 달리 나타난다. 그러나 모형의 인자들의 조합을 적합하게 선택하면 전통적인 선형모형의 분석에서 보다, 결정계수가 더 높게 나타나고 MSE도 더 낮은 좋은 예측 모형으로 나타날 수 있다. 그리하여 고전수업의 만족도를 추정하거나 예측할 때, 의사결정나무 모형. 서포트 벡터 머신 모형, 딥러닝(Deep Leaning)의 심층신경망(Deep Neural Network) 모형을 채택함으로써 자가학습 수행을 자동화하여 기계가 스스로 데이터에서 주요 특징을 추출하여 예측을 수행하면 더 좋은 예측력을 가진 모형이 될 수 있다.
5. 결언
본 연구는 우리나라 대학교 고전수업에 대한 만족도를 분석하기 위해서 전통적으로 사용하는 선형 추정모형 외에도, 우리나라에 있어 아직 전혀 연구가 없는 인공지능을 기반으로 하는 머신러닝과 딥러닝 연구기법에 의해 학습변인 들을 채택하여 수업의 만족도에 대한 분석을 하였다. 그리하여 본 연구의 결과를 요약해서 정리하면 다음과 같다.
첫째, 전통적 선형 모형을 통상적 최소자습법에 의한 회귀분석 결과, 외국인 학생들의 수업만족도가 만족도가 한국인 학생들 보다 낮은 것으로 나왔다. 그러나 가치관 형성, 영화감상의 고전읽기 도움, 고전의 이해에 있어 토론의 유익성 등 3개의 학습변인들은 모두 고전수업의 만족도에 긍정적인 영향을 미치고 있는 것으로 나타났다.
둘째, 인공지능을 기반으로 하는 머신러닝인 의사결정나무에 의한 분류예측을 보면, 수업을 통해 고전을 이해하는 데 도움 여부가 중요한 선행조건으로 의사결정나무의 첫마디가 나누어지고 있다. 수업만족도의 수치예측에서는 고전수업의 삶의 가치관 형성, 영화감상의 도움, 대학생들의 국적, 평소 고전읽기의 중요성과 고전의 필요성 등이 크다고 인식할수록 고전수업의 만족도가 크게 나타났다.
셋째, 서포트 벡터 머신(SVM)에 의한 고전수업의 만족도에 대한 분류예측에서는 학습용 데이터 세트 정확도가 아주 높게 나타났지만, 평가용 데이터 세트 정확도는 낮게 나와 과잉 적합성 문제가 나타났다. 그러나 서포트 벡터 머신 회귀 모형으로 예측결과, 모형의 인자를 적절히 배합하였을 때 학습용과 평가용의 데이터 세트 모두에서 결정계수가 조금 높게 나왔고, RMSE도 낮아 예측모형이 비교적 우수하게 나왔다.
넷째, 딥러닝 모형의 심층 신경망 모형에 의해서 고전수업의 만족도에 대한 회귀예측을 하였을 때, 에포크 수와 배치 크기를 적절히 채택하였을 때 학습용 데이터들 모두 예측오차가 더 작은 것으로 나타나, 수업의 만족도에 대한 서포트 벡터 머신 모형보다 더 좋은 것으로 나타났다.
그리하여 본 연구결과에서 머신러닝 기법들에 의한 고전수업 만족도에 대한 예측결과를 보면, 결정계수와 RMSE 등의 기준으로 살펴볼 때 의사결정나무 모형, 서포트 벡터 머신 모형, 그리고 딥러닝 심층 신경망 모형들은 전통적 모형보다도 수업 만족도 효과 추정에 있어 과잉식별의 문제점을 줄이고 예측력도 높일 수 있는 더 나은 모형이 될 수 있다.
이와 같이 본 연구는 전통적 모델의 기법과는 달리 최근 외국에서 도입되기 시작한 머신러닝과 딥러닝 등의 기법을 도입하여 고전수업의 만족도 효과에 대해 좀 더 정확하게 추정함으로써 향후 고전교육과 수업을 좀 더 효과적으로 지원하기 위한 정책적 시사점을 제공할 수 있다.
그러나 본 연구는 분석대학과 지역을 확대하고 분석대상을 더 많은 자료를 수집하여 사용하면, 좀 더 엄밀한 분석과 해석을 할 수 있을 것이다. 그럼에도 불구하고 본 연구는 우리나라에서 교육 분야의 학습효과 분석에서 아직 소개조차 거의 없는 머신러닝과 딥러닝 기법 등을 사용함으로써 고전학습변인별 학습효과에 대한 후속연구들을 유발하고, 대학생들의 고전과목에 대한 교육정책에 대해서도 시사점을 제공할 수 있을 것이다.

![[그림 1]](/upload//thumbnails/kjge-2023-17-3-25-gf1.jpg)